顔妻です。
今回は株のチャートや統計の教科書でたまに見かける箱ひげ図についてRを使った実例を交えて説明します。なかなかとっつきにくい人もいると思いますが、見方や実例も織り交ぜて説明をしていきます。
箱ひげ図の利用シーン
アイディア次第ではいろいろな使い方ができると思いますが、大まかには以下のシーンで使われることが多いのでないでしょうか?
- 分析のとっかかりとして
- 代表値からは見えてこない変数の全体像を可視化して確認したいとき
- 変数をセグメント別に比較しながら分布を確認したいとき
データの性質がわかっていないときは本当によく使う印象です。ヒストグラムの方が分布の傾向を掴むにはいいと思うのですが、いきなりヒストグラムを作ると左端だけ、右端だけの異様に高い棒ができてあとは地面みたいになってしまって逆にわかりずらいことがあります。なので、あえて粗い粒度で見ることのできるこちらから先にみることをおすすめします。そして、分析をやっていると見過ごしがちなデータの全体像を可視化して把握できるというのは非常にポイントが高いです。
箱ひげ図の見方
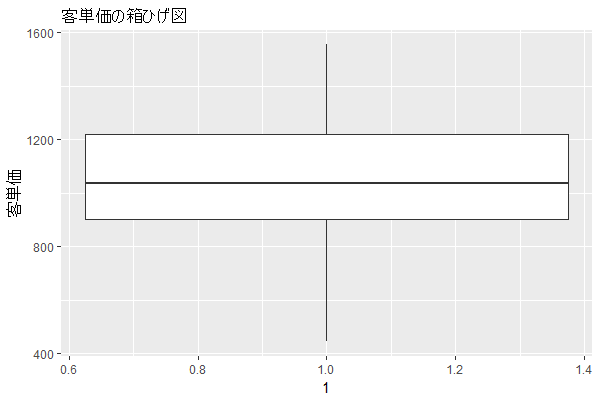
さて、実際の見方についてです。以下の図をご覧ください。
それぞれの項目について説明をしていきます。まず、中央値ですがこれはデータを並べた時に半分の50%のところに来る数値のことです。データの数が奇数の場合の真ん中はすぐわかると思いますが、偶数の場合は、数値をならべてちょうど真ん中にくる値の前後を足して/2したものになります。なので1~100の場合は(50+51)/2=50.5になります。
次は第一四分位点、第三四分位点です。この数値はデータを並べたときに小さい値から数えて、25%、75%に来る値のことです。第二はとなると思いますが、中央値が第二四分位点になります。
それでは極値ですがこれはデータ最小値、最大値付近の数値になります。厳密にどこまでというのはここでは割愛しますが、大体そのあたりと思っていてください。また、外れ値はこの極値と最小値、最大値の間にある数値のことです。
ちなみに、外れ値が存在しないことがありますが、そのときには極値のあたりが最小値、最大値に相当します。では極値が存在するときはどんなときかといいますと、第一四分位点、第三四分位点の間の四分位範囲を大きく離れたときにでてきます。
箱ひげ図の作り方[R]
それではRを用いた作り方です。このShopDataをダウンロードして、Rへのimportまでを済ませてください。また、ggplot2をRにインストールしていない方はパッケージのインストールも済ませておいてください。
先ほどのデータを使って、上記を実行すると以下と同じものができると思います。
箱ひげ図の利用例
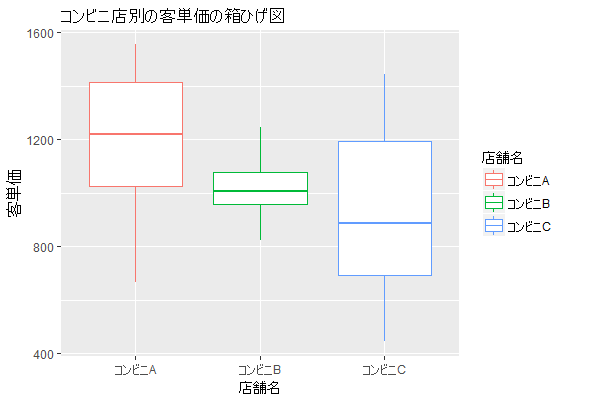
次はより実践的な利用例に移りましょう。先ほどのデータを使って店舗ごとの平均値を算出すると以下になります。
| コンビニA | コンビニB | コンビニC |
| ¥1,210 | ¥1,020 | ¥921 |
どうでしょうか?このデータを見る限り、コンビニAの客単価が高く、コンビニCの客単価が低いようです。このデータを見る限りだとコンビニCのお客さんはあまり物を買ってくれない印象があります。
本当にそうでしょうか?
先ほど使ってみた箱ひげ図を使って可視化して全体像を把握してみましょう。
上記のコードを実行して可視化したものが上記になりますが、先ほどの平均値の比較とはずいぶんと違った印象を受けるのではないでしょうか?箱ひげ図の見方を思い出しながら改めてデータの全体像をみると、コンビニAの平均客単価は1210円でしたが700円位の人がいたり、1400円の人もいたりと、コンビニCは一番客単価が低いところでしたが、他の店舗と比べて単価に幅があるようです。平均値での客単価比較が一括りに誤ってなんてことは思いませんが、この可視化した情報からだと、客層のイメージや種類等のイメージを掴むことができそうですね。
箱ひげ図の使い方・作り方のまとめ
いかがでしたか?実例のところでも少し触れましたが、代表値だけをみるだけでは見えてこなかったデータの全体像を掴む重要性やそれをセグメント毎に比較することでどれだけの示唆がでてくるか少しは理解いただけたのではないでしょうか。確かに少し手間はかかると思いますが、今後データ分析をする機会があったときには遠回りに見えるかもしれませんが箱ひげ図を使った可視化から初めてみてはどうでしょうか?