顔妻です。
今回はヒストグラムについてです。
分析をやっている人でこのグラフを知らないという人がいたらちょっと疑ったほうがいいかもしれないです。そして、それ位どの分析者もお世話になっている可視化方法の一つではないでしょうか。そんなよく使うこのグラフについて整理も兼ねてご紹介をさせて頂きます。
ヒストグラムの利用シーン
個人的に整理をすると以下のようなシーンで使うことが多い気がします。
- 分析の手始めで変数のイメージを掴むため
- 変数がどのような形の分布になっているか把握したいとき
- 変数がどのような傾向を持っているかを確認したいとき
特に分析の手始めでは多用する印象がありますね。そして、予測モデルを作ったり、分類器を作るときの前段階や後段階で分布の形を確認したいときにも使ったりもします。
ヒストグラムの見方・作り方
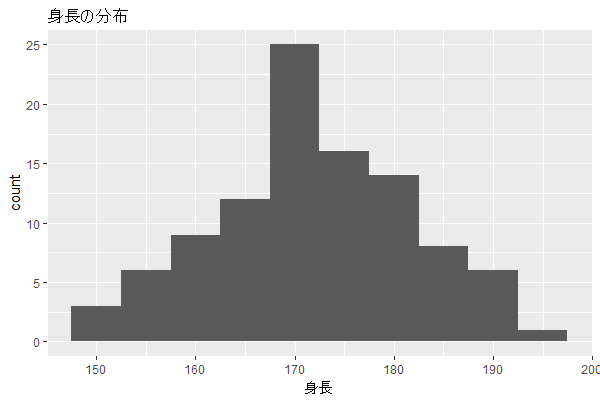
それでは、見方についてです。今回はこのTallのデータを使ってみましょう。このデータはとあるクラスの架空の身長データが100人分はいっています。それでは、いつものようにRにデータのインポートを済ませておいてください。
インポートしたデータを使ってRでスクリプトを読ませると上記の図が出ると思います。今回の可視化の方法は、身長を5刻みで分類し、その間の階級に含まれた身長の数を数えて可視化しています。より具体的には150cm以上~155cm未満が○件、155cm以上~160cm未満が○件、、、といった具合でその階級値に含まれる件数もわかります。
そして、このグラフの読み取りですが、「170cmの区間が最も多く、身長が高くなるにつれて件数が下がり、同様に170cm区間より身長が低くなると件数が下がっていく。」、「分布の形が正規分布のように当てはまりそうな形をしていそうだ。」こんなことを捉えることできそうです。
他の言語を詳しく知らないのであまり大きなことは言えませんが、Rは便利ですよね。スクリプトの「binwidth = 5」このイコールの右側が階級の区間になるのでこれに合わせてヒストグラムを作成してくれます。
ヒストグラムの利用例
見方・作り方がわかったところでより別の例を使って、より実務で出くわしたときに使えそうな読み取りに挑戦してみましょう。
次はWorkingtimeこのデータを使います。これは架空の会社の社員100人分の労働時間データです。実務で言われたら本当に困ってしまうのですが、このデータから何か言えないかと無茶ぶりされたとします。
腕の見せ所というか、仕事を振るのに目的がはっきりしなくていいだろうかと思いますが、そこは課題設定も役割だと割り切って進めましょう。
とはいえ、本当に何をやったらいいかわからないので、まずは全体像を把握するために要約値をだしてみましょう。
労働時間
Min. :131.6
1st Qu.:150.0
Median :224.8
Mean :214.0
3rd Qu.:264.8
Max. :320.8
平均が214時間と全体でみると、すごく労働時間が長いような気はしませんね。ただ、最大値が320時間だったり、第三四分位点が264時間、第一四分位点が150時間と四分位範囲が広いのが気になります。
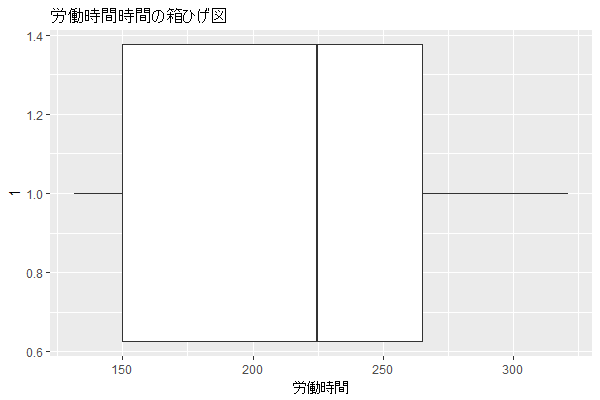
それでは、次は全体像を可視化して確認しましょう。
今回は次ステップも考えて箱ひげ図を横で出してみました。箱ひげ図は要約値を可視化したものになりますので、想定通の形で出てきました。ここまでで読み取れそうなことから提案を仮に考えると、労働時間が長い人がある程度存在はするけど、半分以下は220時間以内だし、労働時間が長い人は一部だけのようだなーと。。。注意喚起を行う位はやったほうがいいかもね。。。
本当にそうでしょうか?労働時間のように自然の力でデータが出来上がらないものはヒストグラムでより詳細にデータを見たほう良さそうです。

箱ひげ図から正規分布のような分布をイメージしていた方はいい意味で裏切られたのではないでしょうか?先ほどの箱ひげ図と見比べるとより違いがわかると思います。
そして、読み取りですが、どうやらこの会社の社員は労働時間にばらつきがあると言うよりも、そもそもの働き方や労働形態なのか、何かしらの原因で異なる分布ができあがっているようです。
このように二つの山になった原因は他の変数を使ってみないとなんとも言えませんが、原因によって打ち手が異なりそうです。
ヒストグラムの使い方・作り方のまとめ
いかがでしたか?未知のデータを取り扱うときや、変数の要約値を把握するだけでは捉えきれない分布の形を把握することがどうして大事なのかわかっていただけたのでないでしょうか。また、その分布をみることで汲み取れる示唆や仮説が浮かんでくると思います。箱ひげ図同様、ちょっと手間に感じることもあるかもしれませんが損にはなりませんので是非使ってみてください。