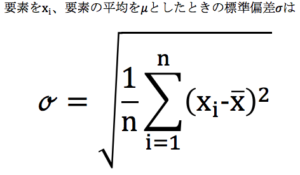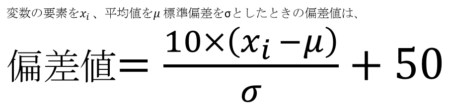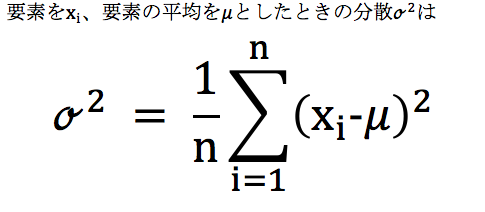標準偏差の作り方・使い方

ビジネスに役立つエクセルと統計学のパッケージが3800円！

顔妻です。

今回は標準偏差の作り方・使い方についてです。単独では使いにくく感じるかもしれませんが特長を捉えると非常に便利な使い方ができますのでご紹介をさせて頂きます。また、特長を捉えるために面倒に感じるかもしれませんが、数式を理解するとより理解が進みますのでこちらも説明させて頂きます。

標準偏差の作り方・意味

まずは、数式からです。

このブログを読んでいた方は、あれどこかの記事と同じ数式じゃないかと思う方もいるかもしれませんが、なかなか鋭い気づきではないでしょうか。というのも以前の記事（http://datasciencehenomiti.com/分散の計算と意味理解/）で説明させていただいた分散の式を平方根したものになるからです。

どうしてそういうことをしているのかと言いますと、以前の分散のままだと、計算プロセスの都合上単位が二乗されたままになっている。そして、二乗されたままのため、値を比較しても実際の値と離れているため参考にしづらい（ほぼできない）。という問題がありました。

そこで、標準偏差では平方根を使って単位を揃えています。これによって、基の要素で算出された平均値からどれだけばらついているかを定量的に把握することができるようなりました。

他にも、変数の分布を正規分布と仮定すると平均値±2σ（2×標準偏差）の間にある要素の値は信頼区間95.4％に収まることが統計的にわかっています。これは乱暴な言い方をすると、平均値±2σに収まっていない値は奇跡に近い異常値やまぐれの可能性があるとということです。（今回は標準偏差の使い方や意味にスコープを絞るため正規分布や信頼区間についてはこの記事では割愛しますが、なんらかの実務で利用する方は必ず目を通してください。）ちなみに平均値±1σは信頼区間68％で収まることが知られています。

標準偏差の使い方① 　〜偏差値〜

それでは実際の使い方についてご紹介です。皆さんは偏差値という言葉をご存知でしょうか？大学や中学・高校なでで受験をされた方は何度も聞いた言葉だと思います。この偏差値ですが、標準偏差がわかると導き出すことができるようになります。式は以下です。

数式だけだとアレルギーがでるだけなので、PaperTestこのデータを使って実際に計算をしてみましょう。

Name	Score	平均値	標準偏差	偏差値
A	82	65.43	19.37	58.55
B	46	65.43	19.37	39.97
C	54	65.43	19.37	44.10
D	49	65.43	19.37	41.52
E	54	65.43	19.37	44.10
F	77	65.43	19.37	55.97
G	96	65.43	19.37	65.78

いかがでしょうか？得点を偏差値に直すと以外と大したことないようにみえるのではないでしょうか？特にGさんは満点に近い得点をだしているにも関わらず、偏差値に直すと約66とそこまで大きく離れているようにはみえないようです。

私たちは色々な値を見比べることが多いと思いますが、その時には大体このくらいというのが頭の中にあったりします。もちろん、感覚値をもつことはデータ分析で違和感に気づいたりするために非常に大事ですが、一方で、その感覚値のせいでデータを歪んでみてしまうことも多いと思います。

実際Gさんはこのクラスでトップの点数、かつ、満点近くですが、偏差値をみるとダントツの点数をとっているとは言えなさそうです。このように、感覚値を排除してデータをみることが分析をするうえで重要ですので、もし、相対的な評価を行う際には是非活用してみてください。

標準偏差の使い方②　〜マッピングで利用する〜

今回はもうひとつご紹介をさせてください。ShopDataこのデータを使ってください。

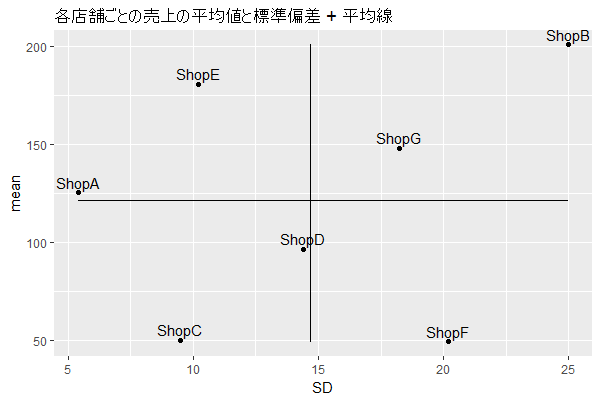
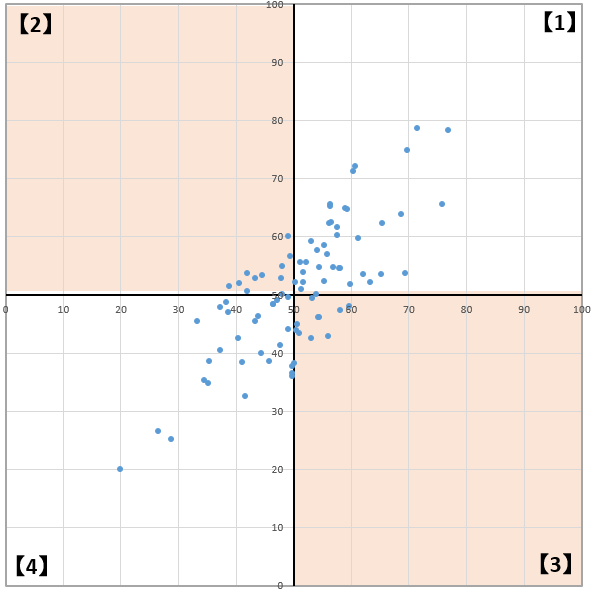
この図は縦軸に各店舗の売上平均、横軸に売上の標準偏差をとった散布図にとり各店舗のポジショニングマップになります。なんのポジションを表現しているかといいますと、どの店舗が売上が高く、そして管理コストがかかりそうかを表現しています。

例えば、標準偏差のばらつきが多いということは一日の販売数量だったり、働くメンバーの数だったりが日によって異なると思います。平日と休日位の違いであれば問題はないのですが、そうでなかった場合、左上のゾーンは安定して売上を出せている店舗、右上は売上こそ平均して高いものの、ばらつきが相対的に大きく管理コストが高くついていると捉えることができそうです。また、この位の標準偏差であれば許容の範囲内かもしれませんが、値が大きくなりすぎている店舗は早めにフォローが入ったほうがいいかもしれません。