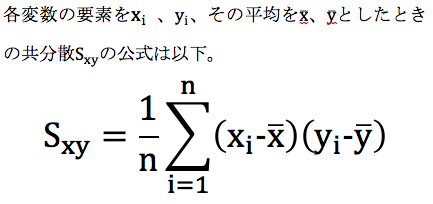顔妻です。
今回は共分散についてです。この値は統計学を学び始めると必ずでくわす相関係数で使われていますが、公式のままに計算をしているだけ、もしくは、R等で手計算を行わないため、そういえばそんな値もあったという人も多いのではないでしょうか？今回はこの値の意味合いを中心に説明し、Rを使った計算にも触れていきます。
共分散の意味
この公式の意味ですが、変数Xの偏差と変数Yの偏差を掛け合わせた値を足し合わせて、要素の個数で割っています。
そして、より具体的に考えたとき、各変数の偏差を掛け合わせた結果のパターンは以下になります。
【1】
の両方が正の値のとき。
【2】が正の値、が負の値のとき。
【3】が負の値、が正の値のとき。
【4】の両方が負の値のとき。
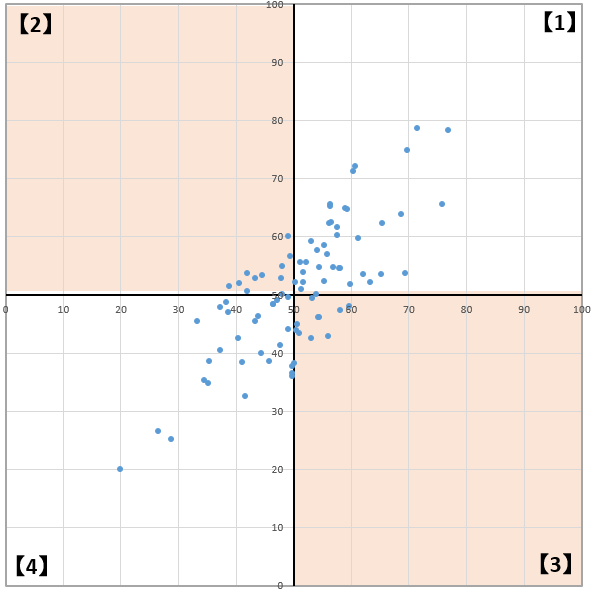
そして、これらの計算結果を足し上げると【1】【4】が正の値、【2】【3】が負の値になります。
ここで共分散はこの計算結果を足し上げてから要素の数で割ります。ここが大事なポイントで計算結果を足し上げた時点で正の値（【1】【4】）が多いときは、その合計も正の値になり、合計した値が負の値（【2】【3】）が多くなるときは合計も負の値になります。（正確にはどちらもなりやすくなります。）
少しイメージがしづらいので、２変数を可視化した散布図を例にとってみてみましょう。
先ほどの計算パターンと照らし合わせてみるとより理解が深まるのではないでしょうか。つまり、共分散は２変数を可視化したときの可視化をうまい具合に表現したものになります。
共分散のRの出力
それではRを使った共分散にも触れてみたいと思います。
このdataをインポートしておいてください。
「var(data$para01,data$para02)」だけでいいのではないか？という方もいらっしゃると思いますが、Rでの「var」は不偏共分散を出力しています。このため、(n)/（n-1）の影響をなくすために「(length(data$para01)-1) / length(data$para01) 」を掛け合わせています。
共分散のまとめ
共分散は散布図の形を定量化しているということに対してイメージが進んだのではないでしょうか。特に相関係数を公式どおりに計算していた方は相関係数のイメージがだいぶついたと思います。相関係数を計算するだけであれば、この意味をわかっていなくても出すことはできます。ただ、今後統計を学ぶ機会がありそうであれば、数式の意味を理解することも大事なポイントの一つになりますので是非他の場面でもトライしてみてください。
