Rで行う因子分析のやり方です。ここでは探索的因子分析にと言われたりするものを取り扱います。因子分析は多くの変数から無相関の共通因子を求める方法です。ここから因子同士の影響具合を読み取っていくこともできます。
準備
今回は因子分析のテストのために、以下で公開されているデータを利用します。
http://www1.doshisha.ac.jp/~mjin/data/
d <- read.csv("factanaldata.csv")
dim(d)
head(d)
## X A B C D E F G H I J K
## 1 1 77 48 28 53 20 16 24 29 17 46 15
## 2 2 100 49 15 50 19 14 21 23 15 31 10
## 3 3 62 32 27 50 21 17 18 24 17 40 15
## 4 4 99 41 15 29 12 12 26 14 14 20 13
## 5 5 94 56 24 43 18 15 25 21 17 37 12
## 6 6 66 50 21 51 17 17 24 23 21 34 13
| A | 検査1 | 円打点検査(○の中に点を打つ検査) |
| B | 検査2 | 記号記入検査(記号 を記入する検査) |
| C | 検査3 | 形態照合検査(形と大きさの同じ図形をさがしだす検査) |
| D | 検査4 | 名詞比較検査(文字・数字の違いを見つける検査) |
| E | 検査5 | 図柄照合検査(同じ図形を見つけだす検査) |
| F | 検査6 | 平面図判断検査(置き方をかえた図形を見つけだす検査) |
| G | 検査7 | 計算検査(加減乗除の計算を行う検査) |
| H | 検査8 | 語意検査(同意語かまたは反意語を見つけだす検査) |
| I | 検査9 | 立体図判断検査(展開図で表された立体形をさがしだす検査) |
| J | 検査10 | 文章完成検査(文章を完成する検査) |
| K | 検査11 | 算数応用検査(応用問題を解く検査) |
スクリープロット
因子分析を利用して作る共通因子の数は探索的になりますが、どの程度までが適切かをはかるためにスクリープロットと呼ばれるものを作ります。そしてx軸のindexが共通因子の数でy軸の固有ベクトルの値が1以上あれば適切な数として使えると言われています。
d_cor <- cor(d[,2:12])
d_cor_eigen <- eigen(d_cor)
plot(d_cor_eigen$values,type = "b")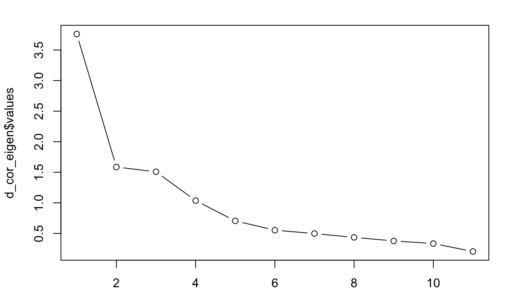
因子分析の実行
先ほどのスクリープロットをみながら今回は要素を4にして実施しました。
CATB50.fa <- factanal(d, factors = 4, scores = "Bartlett")
CATB50.fa
##
## Call:
## factanal(x = d, factors = 4, scores = "Bartlett")
##
## Uniquenesses:
## X A B C D E F G H I J K
## 0.831 0.005 0.692 0.705 0.405 0.478 0.038 0.545 0.449 0.520 0.314 0.424
##
## Loadings:
## Factor1 Factor2 Factor3 Factor4
## X 0.396
## A 0.175 0.976
## B 0.261 0.371 0.304
## C 0.315 0.403 0.138 -0.120
## D 0.664 0.286 0.260
## E 0.594 0.300 -0.272
## F 0.199 0.960
## G 0.113 0.661
## H 0.663 0.190 0.256
## I 0.295 0.570 0.254
## J 0.803 -0.106 0.149
## K 0.302 0.199 -0.131 0.654
##
## Factor1 Factor2 Factor3 Factor4
## SS loadings 2.218 1.777 1.330 1.268
## Proportion Var 0.185 0.148 0.111 0.106
## Cumulative Var 0.185 0.333 0.444 0.549
##
## Test of the hypothesis that 4 factors are sufficient.
## The chi square statistic is 23.58 on 24 degrees of freedom.
## The p-value is 0.486
因子分析結果の可視化
先ほどの結果から共通因子を可視化して、元の変数の関連性をみます。すると各因子の特徴を掴めます。
par(mfrow = c(2,2))
barplot(CATB50.fa$loadings[,"Factor1"],main = "Factor1")
barplot(CATB50.fa$loadings[,"Factor2"],main = "Factor2")
barplot(CATB50.fa$loadings[,"Factor3"],main = "Factor3")
barplot(CATB50.fa$loadings[,"Factor4"],main = "Factor4")
par(mfrow = c(1,1))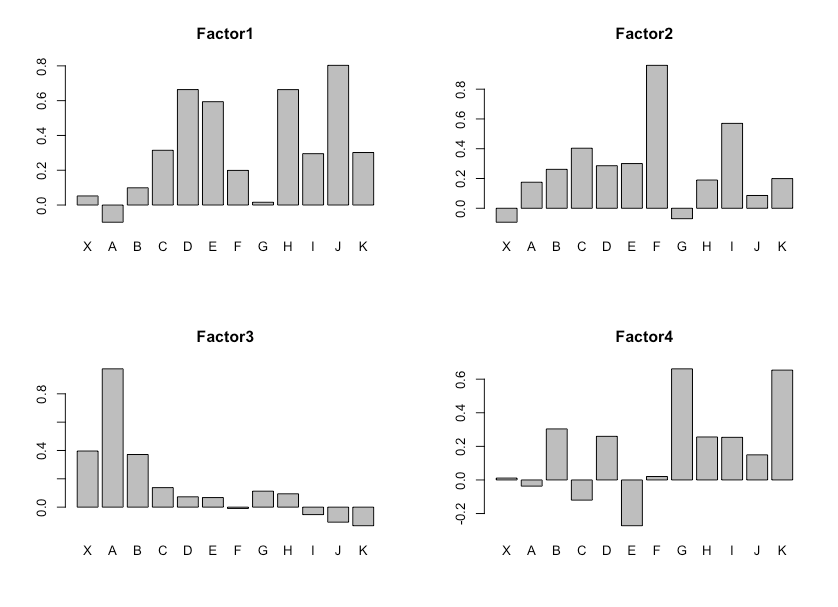
次は作り出した共通因子をもとに回答者の分布を確認します。すると、回答者が先ほど確認した共通因子のどのよう因子の影響を強く受けていそうかがわかります。
plot(CATB50.fa$scores[,1:2],type = "n")
text(CATB50.fa$scores[,1:2],rownames(CATB50.fa))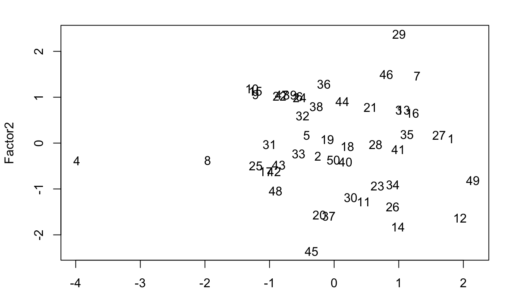
因子分析の精度
最後に累積因子負荷量をみます。1に近くなるほど精度がよいとみることができます。
CATB50.fa$criteria
## objective counts.function counts.gradient
## 0.5681002 19.0000000 19.0000000