正規分布
x <- seq(-4, 4, 0.1)
plot(x = x,y = dnorm(x, -2, 1),type = "b",ylim = c(0,1))
par(new = T)
plot(x = x,y = dnorm(x, 0, 1),type = "b",ylim = c(0,1),col = 2)
par(new = T)
plot(x = x,y = dnorm(x, 0, 2),type = "b",ylim = c(0,1),col = 3)
par(new = T)
plot(x = x,y = dnorm(x, 0, 0.5),type = "b",ylim = c(0,1),,col = 4)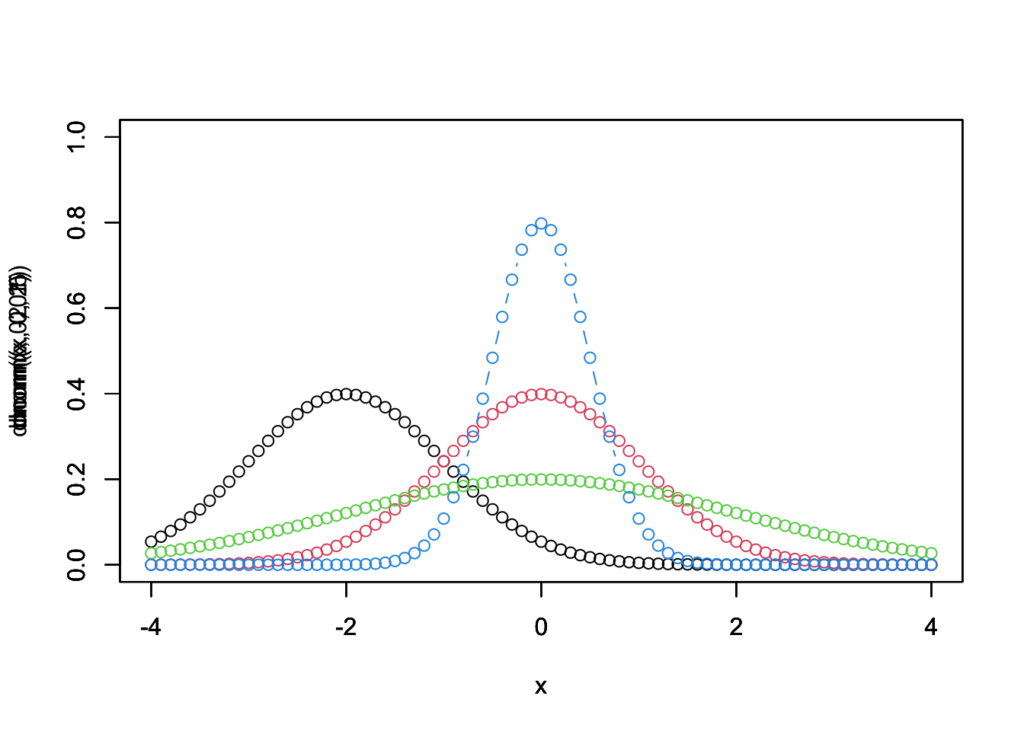
二項分布
i <- seq(1,30)
plot(x = i,dbinom(x = i,size = 30,prob = 0.2),type = "b",ylim = c(0,0.5))
par(new = T)
plot(x = i,dbinom(x = i,size = 30,prob = 0.5),type = "b",col = 2,ylim = c(0,0.5))
par(new = T)
plot(x = i,dbinom(x = i,size = 30,prob = 0.1),type = "b",col = 3,ylim = c(0,0.5))
par(new = T)
plot(x = i,dbinom(x = i,size = 100,prob = 0.2),type = "b",col = 4,ylim = c(0,0.5))
legend_name <- c("size = 30,prob = 0.2","size = 30,prob = 0.5","size = 30,prob = 0.1","size = 100,prob = 0.2")
legend(x = 15,y = 0.5,legend = legend_name,col = c(1:4),lwd=3)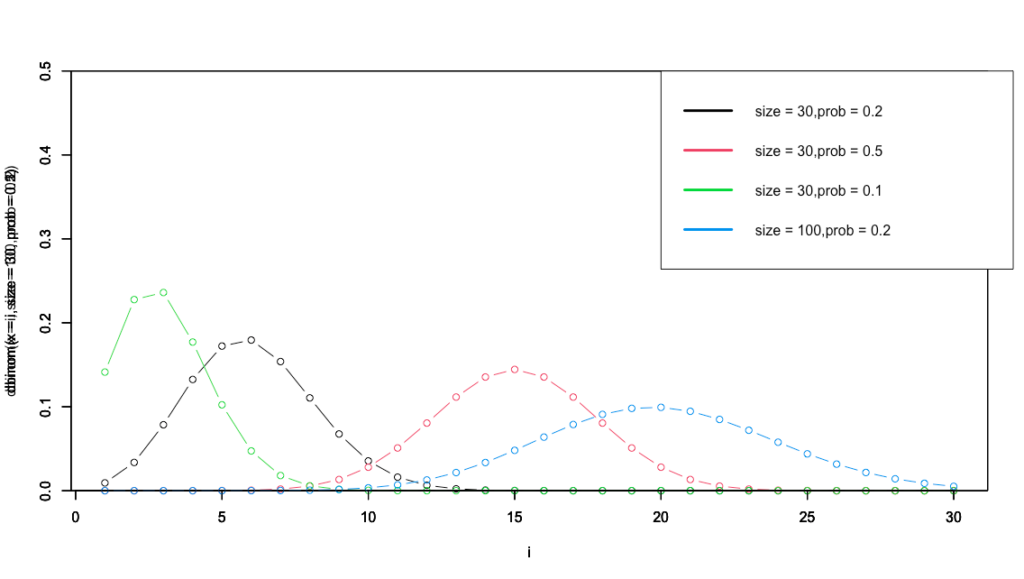
par(mfrow = c(2,2))
plot(x = i,dbinom(x = i,size = 30,prob = 0.2),type = "b",ylim = c(0,0.3))
plot(x = i,dbinom(x = i,size = 30,prob = 0.5),type = "b",col = 2,ylim = c(0,0.3))
plot(x = i,dbinom(x = i,size = 30,prob = 0.1),type = "b",col = 3,ylim = c(0,0.3))
plot(x = i,dbinom(x = i,size = 100,prob = 0.2),type = "b",col = 4,ylim = c(0,0.3))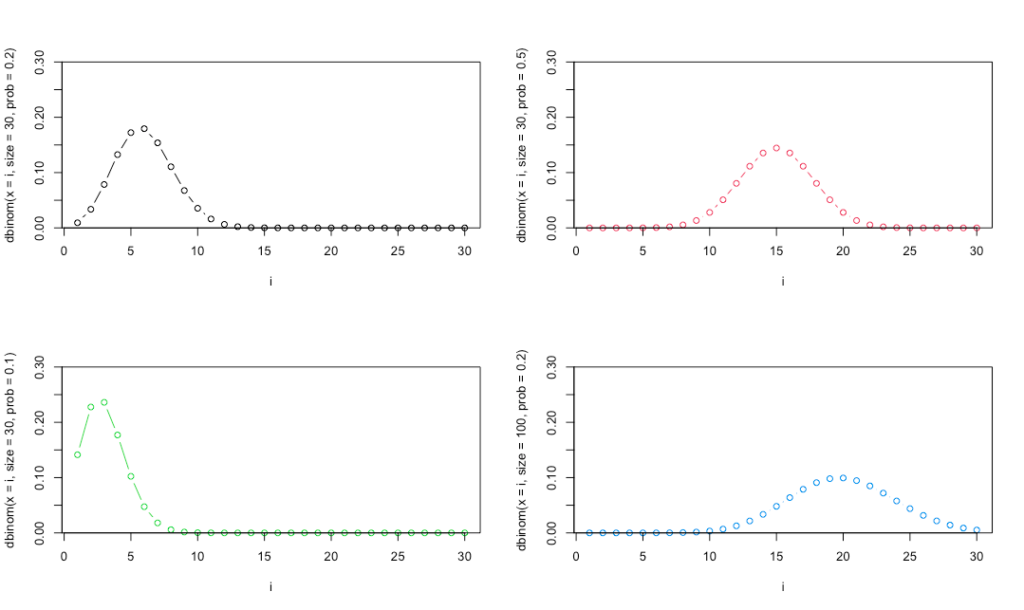
ポアソン分布
- 決まった試行回数k回の中でlambdaは決まった期間や区間の間で起きる平均発生数。
- ポイントはこの平均発生数なので、
- 例
- 1日に平均5回成約する営業員が60件訪問した場合の成功率は0.2程度のような見方
ポアソン分布
rpois(n = 30,lambda = 5)
x <- seq(1,60)
par(mfrow = c(2,2))
plot(x, y = dpois(x = x, lambda = 1), type = "b")
plot(x, y = dpois(x = x, lambda = 5), type = "b",col = 2)
plot(x, y = dpois(x = x, lambda = 10), type = "b",col = 3)
plot(x, y = dpois(x = x, lambda = 30), type = "b",col = 4)
par(mfrow = c(1,1))負の二項分布
- 統計的に独立なベルヌーイ試行を続けて行ったときに、r 回の失敗をする前に成功した試行回数の分布。成功と失敗の定義は逆になることもある。
- 同様に、統計的に独立なベルヌーイ試行を続けて行ったとき、r 回の成功を得るのに必要な試行回数の分布。
- 数学的に、1番目の意味でのベルヌーイ試行の r を整数から実数に拡張して考えるもの。
x <- seq(1,60)
par(mfrow = c(2,2))
plot(x, y = dnbinom(x = x,size = 1,prob = 0.1), type = "b")
plot(x, y = dnbinom(x = x,size = 1,prob = 0.3), type = "b",col = 2)
plot(x, y = dnbinom(x = x,size = 1,prob = 0.5), type = "b",col = 3)
plot(x, y = dnbinom(x = x,size = 1,prob = 0.7), type = "b",col = 4)
par(mfrow = c(1,1))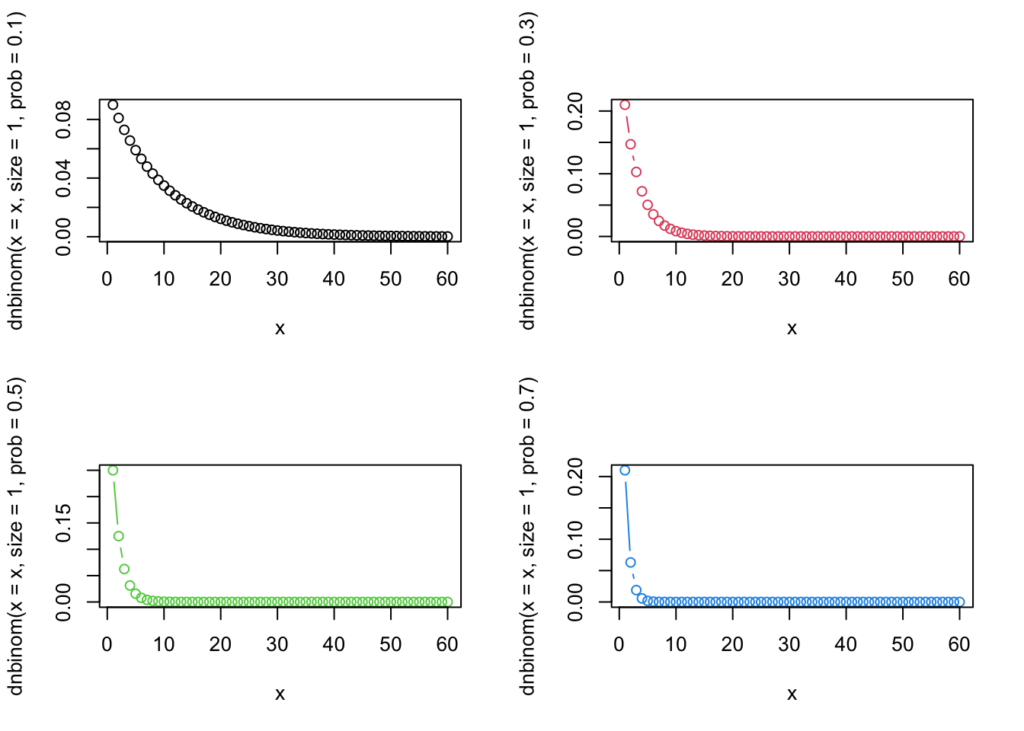
- 以下は事象rが10回起きたパターン
par(mfrow = c(2,2))
plot(x, y = dnbinom(x = x,size = 10,prob = 0.1), type = "b")
plot(x, y = dnbinom(x = x,size = 10,prob = 0.3), type = "b",col = 2)
plot(x, y = dnbinom(x = x,size = 10,prob = 0.5), type = "b",col = 3)
plot(x, y = dnbinom(x = x,size = 10,prob = 0.7), type = "b",col = 4)
par(mfrow = c(1,1))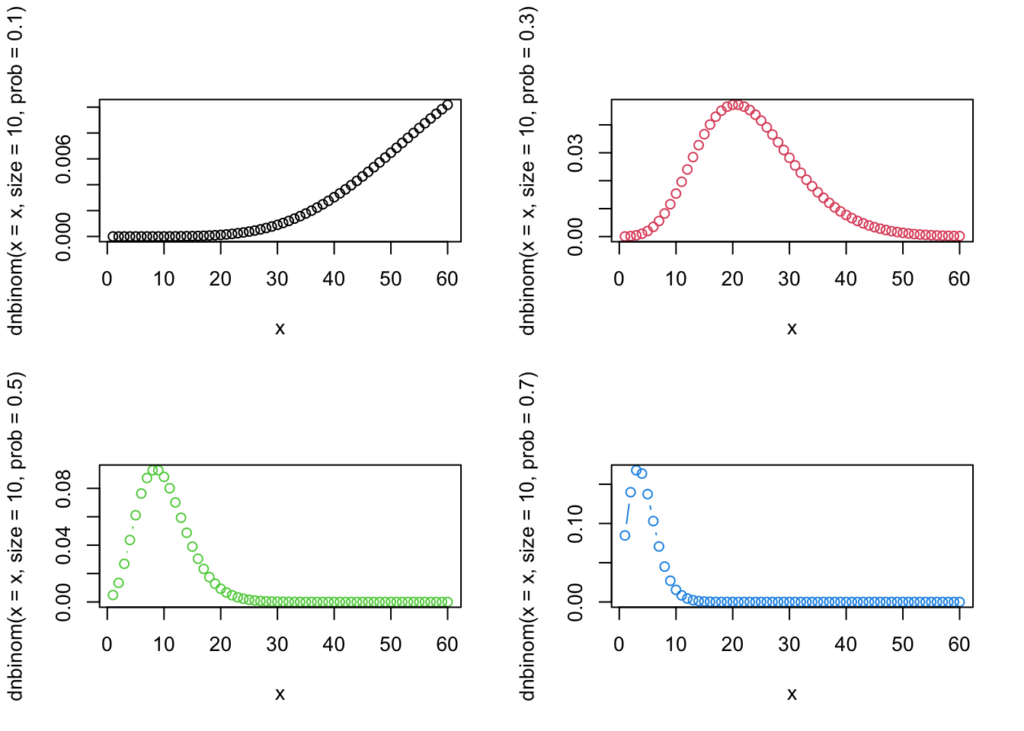
カイ2乗分布
例題1)ここで、分布を利用した統計推理をしてみることにします。いまあるコーヒー喫茶店にコーヒーを飲みにやって来るお客さんの人数は1日に平均16人であることがわかっている場合、32人以上のお客さんがこの店にやって来る日数は1ヶ月のうちに何日あるかを推定してみて下さい。また、1日に8人以下しかお客さんが来ない日数は1ヶ月のうち何日あるでしょうか。
(解答)分布の平均は自由度に等しいから、この場合となります。
par(mfrow = c(2,2)) px <- seq(1,60)
x
par(mfrow = c(2,2))
plot(x, y = dchisq(x = x,df = 1,ncp = 0), type = "b")
plot(x, y = dchisq(x = x,df = 5,ncp = 0), type = "b",col = 2)
plot(x, y = dchisq(x = x,df = 10,ncp = 0), type = "b",col = 3)
plot(x, y = dchisq(x = x,df = 30,ncp = 0), type = "b",col = 4)
par(mfrow = c(1,1))lot(x, y = dchisq(x = x,df = 1,ncp = 0), type = "b") plot(x, y = dchisq(x = x,df = 5,ncp = 0), type = "b",col = 2) plot(x, y = dchisq(x = x,df = 10,ncp = 0), type = "b",col = 3) plot(x, y = dchisq(x = x,df = 30,ncp = 0), type = "b",col = 4)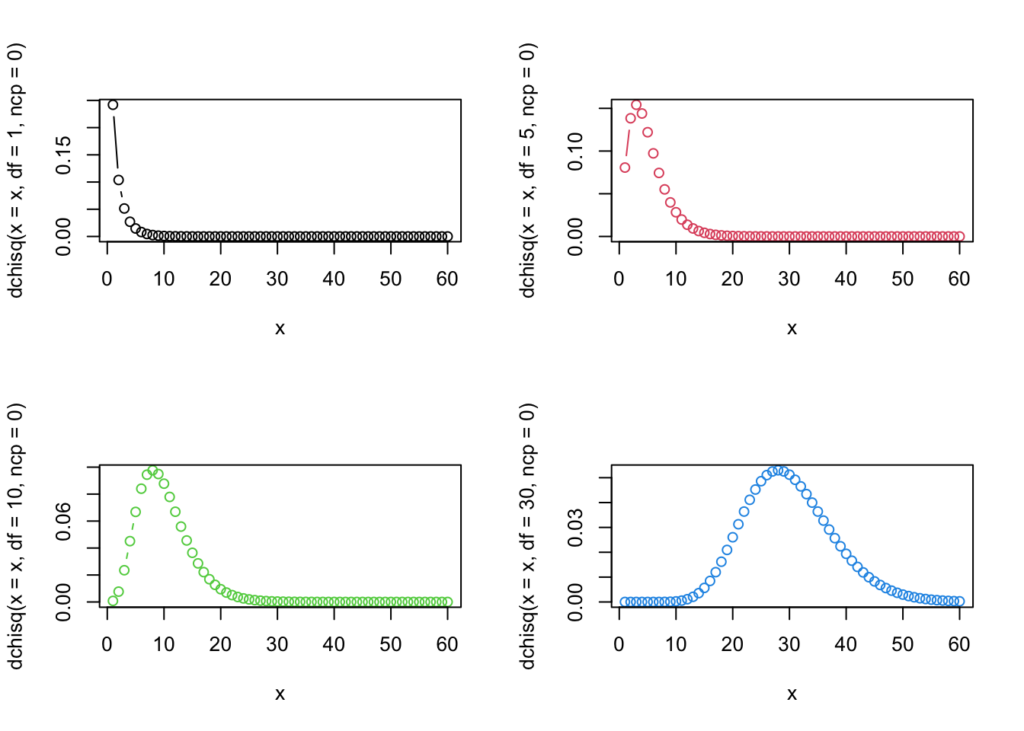
様々な確率密度関数、乱数発生関数
| 分布の総称 | 確率密度関数 | 乱数発生関数 |
|---|---|---|
| 一様(Uniform)分布 | dunif(x, min=0, max=1,・・・) | runif(n, min=0, max=1) |
| 二項(Binomial)分布 | dbinom(x, size, prob,・・・) | rbinom(n, size, prob) |
| ポアソン(Poisson)分布 | dpois(x, lambda,・・・) | rpois(n, lambda) |
| 正規(Normal)分布 | dnorm(x, mean=0, sd=1,・・・) | rnorm(n, mean=0, sd=1) |
| カイ2乗(Chi-square )分布 | dchisq(x, df, ncp=0,・・・) | rchisq(n, df, ncp=0) |
| t分布 | dt(x, df,・・・) | rt(n, df) |
| F分布 | df(x, df1, df2,・・・) | rf(n, df1, df2) |
| ガンマ(Gamma)分布 | dgamma(x, shape,・・・) | rgamma(n, shape) |
| ベータ(Beta)分布 | dbeta(x, shape1, shape2,・・・) | rbeta(n, shape1, shape2) |
| 対数正規(Lognormal)分布 | dlnorm(x, meanlog = 0, sdlog = 1,・・・) | rlnorm(n, meanlog = 0, sdlog = 1) |
| ロジスティック(Logistic)分布 | dlogis(x, ・・・) | rlogis(n) |
| 指数(Exponential)分布 | dexp(x, rate = 1, ・・・ ) | rexp(n, rate = 1) |
| 負二項(Negbinomail)分布 | dnbinom(x, size, prob, mu,・・・ ) | rnbinom(n, size, prob, mu) |
| 多項(Multinomial)分布 | dmultinom(x, prob, ・・・ ) | rmultinom(n, size, prob) |
| 幾何(Geometric)分布 | dgeom(x, prob, ・・・ ) | rgeom(n, prob) |
| 超幾何(Hypergeometric)分布 | dhyper(x, m, n, k, ・・・ ) | rhyper(nn, m, n, k) |
| コーシー(Cauchy)分布 | dcauchy(x,location=0,scale= 1,・・・ ) | rcauchy(n,location=0,scale = 1) |
| ワイブル(Weibull)分布 | dweibull(x,shape,scale=1,・・・ ) | rweibull(n, shape, scale = 1) |