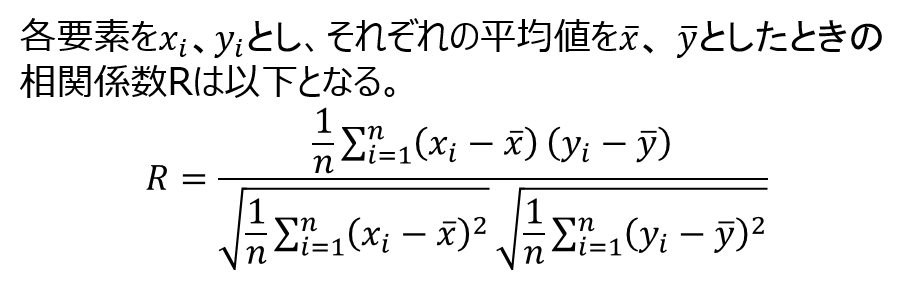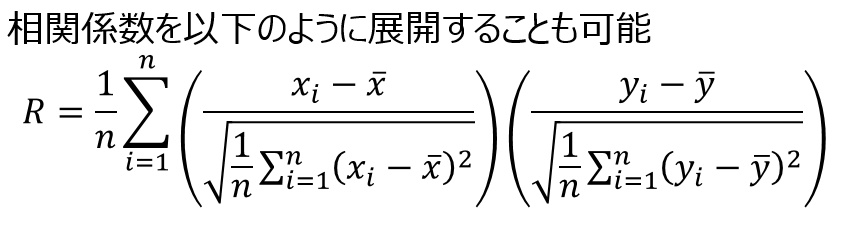顔妻です。
今回は相関係数についです。2変数の直線的な関係性を定量化するこの値についてRを使った計算方法や使い方について説明したいと思います。また、相関係数ではなぜ因果関係を伝えることができないのかについても触れていきます。
相関係数の意味
相関係数の大きな役割は2変数の関係性を定量化できるところです。この数値の計算結果は必ず−1~1の間になり、数値が1に近づくにつれて正の相関が強く、−1に近づくにつれて、負の相関が強くなります。そして、0の場合には相関係数を計算するのに使った変数に相関がないと判断できます。
ここではよりイメージをしやすいようにどのような分布がどの位の相関係数になるかをみていきましょう。
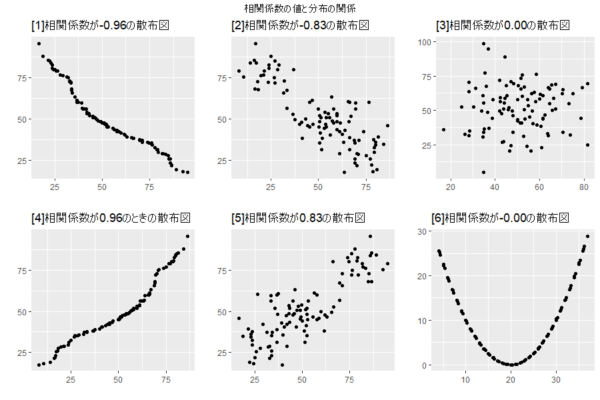
だいぶイメージが掴めたのではないでしょうか。上図のように相関係数が[1][4]の0.96のときや-0.96のときには、ほぼ直線になっています。
また、[2][5]のように±0.83と比較的高いときにはデータの各要素である点が比較的まとまって関係性が強そうに見えます。
[3]の相関係数はほぼ0に近い無相関です。要素同士にまとまりがなく、まんべんなく広がっているのがわかります。ただし、ここで注意して欲しいことがあります。相関係数は性質として直線関係を前提に定量化を行っています。このため、[6]のように計算結果では相関がないように見えても実際には曲線での関係性が見える場合があります。
また、もう一つ注意をして欲しいのが、相関係数の結果は順序尺度として判断するようにして細かな数値の大小で比べないようにしてください。
相関係数の数式理解
数式がかなり並びましたが、この式は要素、x、yとの共分散÷(xの標準偏差×yの標準偏差)となっています。一般的にはこの数式で表現されることが多いですが、以下のように展開したほうがより理解が進むのではないかと思っています。
計算の結果は全く同じですが、こちらの方がだいぶわかりやすいのではないでしょうか?というのも、この数式をみるとどうやら相関係数は標準化したデータの各要素を使って共分散を計算してるようです。(共分散はこちらのリンクでも説明していますのでご参考ください。)
最初の数式ではわかりづらいですが相関係数は標準化した共分散と言えそうです。また、相関係数はあくまで2変数の関係性がどれだけ直線に近いからを数量化したものと解釈できそうです。これこそ、相関係数では因果関係がわからず関係性の強さしかわからないと言われる理由です。
相関係数をRで実行
それでは、実際にRを使って計算していきましょう。Rに標準で組み込まれているirisを利用します。
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | |
| Sepal.Length | 1.00 | -0.12 | 0.87 | 0.82 |
| Sepal.Width | -0.12 | 1.00 | -0.43 | -0.37 |
| Petal.Length | 0.87 | -0.43 | 1.00 | 0.96 |
| Petal.Width | 0.82 | -0.37 | 0.96 | 1.00 |
Rでの実行はとても簡単ですね。
そして、Rで実行した場合には相関行列として上記のように変数同士の相関係数が一度に出力されます。このため、同じ変数同士の相関係数の結果が「1.00」となりその他は変数同士の結果がでてきています。
相関係数の結果の目安とこの読み取りの注意点
相関係数の結果は目安として以下のように言うことがあります。
| 結果の解釈 | 値の範囲 |
| 正の相関がとてもある | 1.0 ~ 0.7 |
| 正の相関がある | 0.7 ~ 0.4 |
| 正の相関がややある | 0.4 ~ 0.0 |
| 相関がない | 0.0 |
| 負の相関がややある | -0.4 ~ -0.0 |
| 負の相関がある | -0.7 ~ -0.4 |
| 負の相関がとてもある | -1.0 ~ -0.7 |
ただし、この解釈はあくまで目安です。データの中身や今まで経緯と比較を考えて解釈する必要がありますので注意をして利用してください。
| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | |
| Sepal.Length | 1.00 | -0.12 | 0.87 | 0.82 |
| Sepal.Width | -0.12 | 1.00 | -0.43 | -0.37 |
| Petal.Length | 0.87 | -0.43 | 1.00 | 0.96 |
| Petal.Width | 0.82 | -0.37 | 0.96 | 1.00 |
改めて先ほどの結果を解釈してみましょう。「Sepal.Length」と「Petal.Length」の相関係数は0.87と関係性がとても強くでているようです。また、「Sepal.Width」と「Petal.Length」の相関係数は-0.43と負の相関がでているとしてデータをみることができそうです。
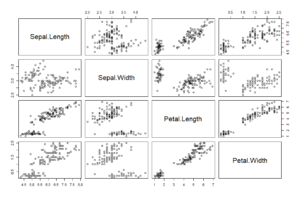
それでは、今度はグラフで可視化した結果をみてみましょう。
相関係数の結果とはまた違った気づきがあるのではないでしょうか?先ほど負の相関がありそうにみえた「Sepal.Width」と「Petal.Length」の組み合わせですがどうやら分布に偏りがあるようです。このため、先ほど相関係数を鵜呑みにしてしまうと誤った解釈となりそうです。
ということで、相関係数をみるときには少し面倒に感じるかもしれませんが、必ず可視化もセットで行うとデータを見誤ることが減ると思います。
相関係数のまとめ
相関係数の数式を覚えるの最初は苦労するかもしれませんが、仕組みを知ればそこまで難しいものではないのではないでしょうか。さらに、数式を理解することは、なぜ相関係数では因果関係を言えないのかを理解するのに非常に役立つと思います。また、実際に使うときには相関係数は可視化もセットで行う。これも大事にして頂ければと思います。