散布図の作り方・使い方

顔妻です。

今日は散布図についてです。マーケティングの本ではそこそこ見かけたりしますが、人によっては普段の分析でなかなか使うシーンが少ないのではないのでしょうか？今回はそんな散布図にスポットを当てたいと思います。

散布図の利用シーン

2変数間の関係性を知るため
予測モデルの作成時・検証時
各要素のポジションを確認するとき

ほとんど、「２変数間の関係性を知るため」に集約されてしまいますが大事だなと思うところを強調の意味も込めてあげてみました。

散布図の見方・使い方

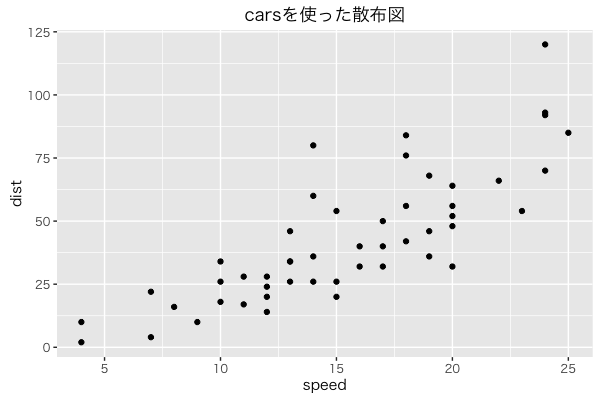
今回はRにもともと組み込まれている「cars」を利用しますので、以下のスクリプトの実行のみで大丈夫です。このデータは車の速度とその速度で急停止したとき止まるまでの距離が測定されています。

どんなデータが可視化されているかといいますと、縦軸が停止までの距離、横軸がスピードです。そして点になっているものはそれぞれの要素です。

このグラフから読み取れることとして、停止までの距離が長くなるときはそれまでのスピードが早いことがみてとれそうです。また、各要素の点がまとまっているようですの正の相関がありそうです。正の相関について、ここでは詳しく説明しませんが、停止までの距離とスピードには関係性がありそうだということが言えそうです。（ありそうだという表現が大事です。）

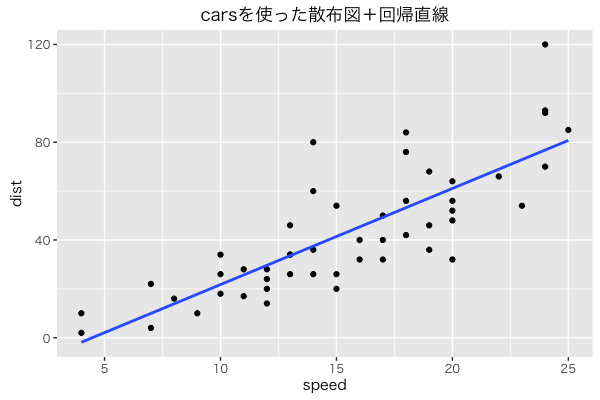
ちなみに、またもや詳細な説明は割愛しますが、参考までに、以下のコードを実行してみてください。

青い線が出てきたと思います。今回引いたこの線は回帰直線と言われるものです。この線は分布の中心を通るように線が引かれます。また、分布の傾向を簡単に知るにはとても便利です。（とりあえず線が引かれるのでばらつきが大きいときミスリードしてしまうので注意をしてください。）

散布図の利用例

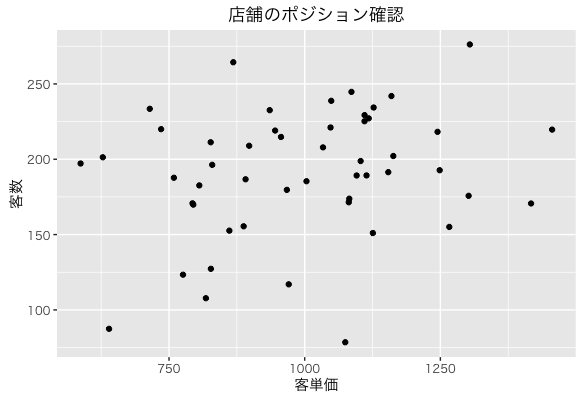
散布図から２変数の関係性をみることができること説明しましたが、次は別の例をお見せしたいと思います。ShopPotitionこのデータをRにimportをして以下のコードを実行してみましょう。

先ほどまでとはうってかわって、この２変数に正の相関や負の相関といった関係性はみれなさそうですね。ただ、そこがいいんです。どうゆうことかといいますと、このデータは各店舗の客数と客単価が入っています。そして、要素がばらついているということは、そのぶんだけ店舗のごとの特長を相対的に洗い出すことができるということです。

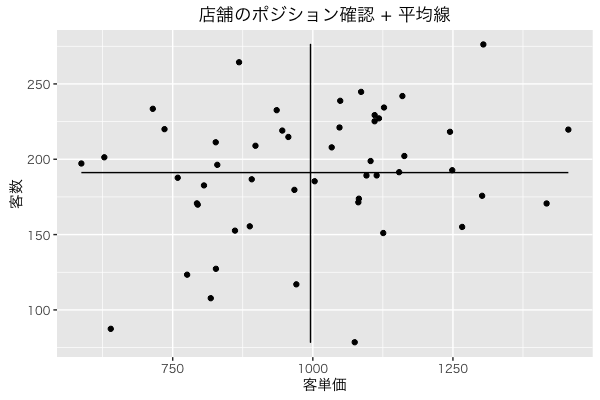
このままでは少しわかりにくいので以下のスクリプトを実行してみてください。

先ほどの図に加えて２本の平均線が加わっています。この線を加えて何が読み取れるかといいますと、客数の線より上で、かつ、客単価の線よりも右のゾーンにある店舗たちですがどうやら相対的に優良そうです。なぜなら「客数 × 客単価 = 売上」だからです。そして、右上のゾーンにある人たちはその額が相対的に多い店舗になります。ここからはよりデータの定性的な面を掘ったり、別の軸で比較したりが必要ですが、同じ客数で客単価が左のゾーン、右のゾーンに分かれているお店は比較しがいがありウキウキしてくるところです笑　そして、左上のゾーンにある店舗は客数は多いのになぜ、客単価が相対的に低いのか？そんなこと感がると仮説出しにつながるのではないでしょうか？また、この話から金のなる木や、PPMなんて言葉を思い起こす人も多いのではないでしょうか。実際比較に使う軸の取り方が異なるだけで似た考えを使えます。