顔妻です。
前回に続いて金相場の予測を行ってみようと思います。
今回は前回と同じデータを使って、金相場の推移データで回帰分析を適用するとどうなるかをみていきたいと思います。
推移の可視化 回帰直線を追加
前回とまったく同じことは省略し、折れ線グラフに回帰直線を追加しようと思います。追加の方法はgeom_smooth(method = lm) +を追加するだけです。
library(tidyverse)
library(glmnet)
theme_set(theme_bw())
d <- read.csv('https://raw.githubusercontent.com/maruko-rosso/datasciencehenomiti/master/data/gold/1540_20220512.csv',encoding = 'UTF-8')
d <- d %>% arrange(as.Date(日付))
#### 回帰直線を追加する ####
d %>%
ggplot(aes(x = as.Date(日付),y = 終値)) +
geom_line() +
scale_x_date(date_breaks = "2 week",
date_labels = "%m/%d"
) +
xlab('日付') +
scale_color_brewer(palette = "Set1") +
geom_smooth(method = lm) +
ggtitle('1540 金相場の推移 回帰直線追加')
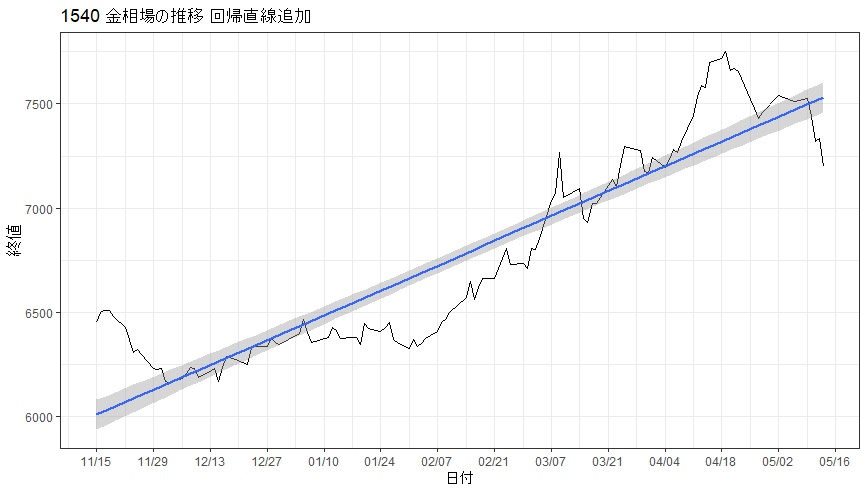
このときの相場データを使うと傾向をとらることはまずまずできていそうなガキがします。グレーの部分は誤差のカバー範囲ですのでこのあたりに収まるとかなり精度の高いデータと言えそうです。
回帰分析の実行
それでは、実際に回帰分析を行いたいと思います。
d_lm <- lm(formula = 終値 ~ as.Date(日付) ,data = d)
summary(d_lm)
# Call:
# lm(formula = 終値 ~ as.Date(日付), data = d)
#
# Residuals:
# Min 1Q Median 3Q Max
# -343.09 -144.59 -6.56 86.66 483.46
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -1.550e+05 6.690e+03 -23.18 <2e-16 ***
# as.Date(日付) 8.501e+00 3.515e-01 24.19 <2e-16 ***
# ---
# Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 199 on 117 degrees of freedom
# Multiple R-squared: 0.8333,
# F-statistic: 585 on 1 and 117 DF, p-value: < 2.2e-16
結果をみると、Multiple R-squared: 0.8333が1に近く、説明変数の日付も***と有意性もかなり高いことがいえそうです。このため、現状の分布においては回帰分析でも十分な予測精度が保てているといえそうです。
重回帰分析の実行
金相場を予測を行うにあたって、未来の日付になればなるほど相場金額があがるというわけではないはずなので、説明変数を追加してみようと思います。今手元にあるデータでよさそう出来高を活用しようと思います。
# 説明変数追加
d_lm_02 <- lm(formula = 終値 ~ as.Date(日付) + 出来高 ,data = d)
summary(d_lm_02)
# Call:
# lm(formula = 終値 ~ as.Date(日付) + 出来高, data = d)
#
# Residuals:
# Min 1Q Median 3Q Max
# -315.7 -143.3 -3.5 112.5 459.8
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -1.421e+05 6.724e+03 -21.137 < 2e-16 ***
# as.Date(日付) 7.815e+00 3.539e-01 22.085 < 2e-16 ***
# 出来高 1.128e-03 2.377e-04 4.746 5.97e-06 ***
# ---
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
# Residual standard error: 182.8 on 116 degrees of freedom
# Multiple R-squared: 0.8604,
# F-statistic: 357.6 on 2 and 116 DF, p-value: < 2.2e-16
結果をみると、Multiple R-squared: 0.8604が1に近く、説明変数の日付と出来高の両方とも***と有意性もかなり高いことがいえそうです。このため、先ほどよりも精度の高い統計モデルが作れたといえそうです。
予測結果の可視化
それでは、先ほどまでに回したモデルを可視化してみましょう。定量的な予測精度はわかりましたが、どの程度もともとのモデルに近くなったかは一度みてみる必要がありそうです。
## モデル結果の格納
d$model_01 <- d_lm$fitted.values
d$model_02 <- d_lm_02$fitted.values
## 可視化
d %>%
ggplot(aes(x = as.Date(日付),y = 終値, col = '金相場1540')) +
geom_line() +
scale_x_date(date_breaks = "2 week",
date_labels = "%m/%d"
) +
xlab('日付') +
scale_color_brewer(palette = "Set1") +
# geom_smooth(method = lm) +
ggtitle('1540 金相場の推移 モデル結果の反映') +
geom_line(aes(y = model_01,x = as.Date(日付),col = 'model_01')) +
geom_line(aes(y = model_02,x = as.Date(日付),col = 'model_02'))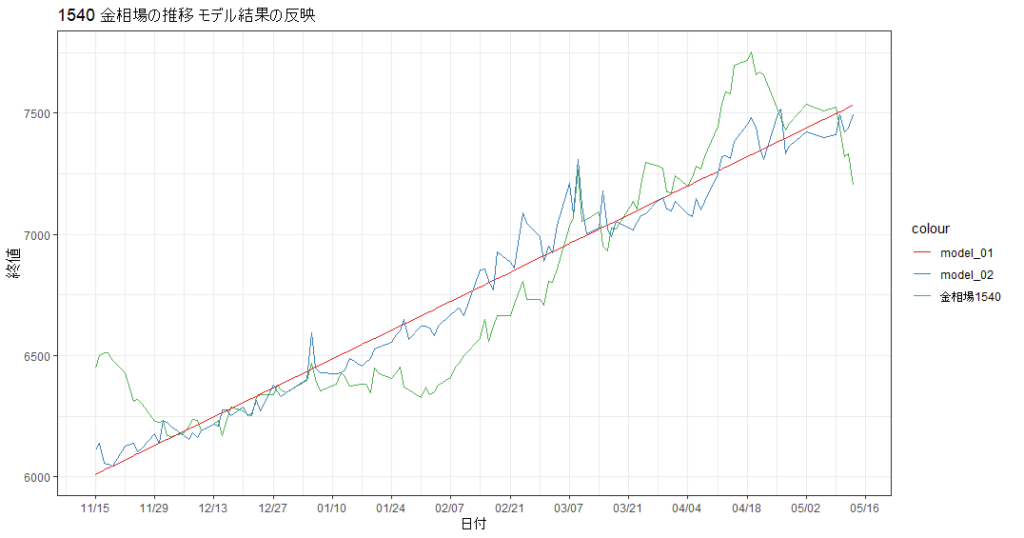
緑がもともとの相場推移です。赤が回帰分析の結果、青が変数を追加した統計モデルになります。これをみると赤の回帰分析の結果は本当に線が引かれただけで予測できたというにはだいぶ乱暴になりそうです。一方で1変数しか追加していませんが、青の重回帰分析結果のほうが相場のうごきに相対的に近いといえそうです。
予測精度検証 RMSE
今後、他のアルゴリズムを利用した予測結果の比較も行うために二乗平均平方根誤差 RMSEによる予測精度もここに記載しておこうと思います。RMSEは予測結果と目的変数(予測したい元の数値)の差をとって、どの程度元の数値と予測結果にズレがあったかを定量的に表現する方法です。比較したときに数値が小さいほど精度が高くなるといえます。
sqrt(sum((d$終値 - d_lm$fitted.values) ^2) / length(d$終値))
# [1] 197.2769
sqrt(sum((d$終値 - d_lm_02$fitted.values) ^2) / length(d$終値))
# [1] 180.5263結果をみると、説明変数を加えた統計モデルのほうがより精度が高いことが別の精度検証方法でもわかったといえそうです。金相場はこの他にも為替や日経平均や他のコモディティといったものにも影響を受けそうなため次回はこの辺りの解析を進めていき、予測精度の高いものを実現するのもありかもしれませんね。