金の株式相場をAIで予想する３

顔妻です。

前回に引き続き金の株式相場をAIで予想する予測をやっていこうと思います。前回は変数を増やした場合にどの程度予測精度があがるのかを検証してみました。今回は前回に引き続き、変数を増やした場合にどの程度精度があがるのかを検証してみたいと思います。

過去記事

今回、特徴量として増やした変数は以下の９つです。

金相場(1540)の出来高
ドル円の為替
NYダウの終値
NYダウの出来高
長期国債先物_終値
長期国債先物_出来高
日経平均_終値
日経平均_出来高

金相場との相関関係を確認する

ビッグデータを分析するというにはまだまだ変数は少ないですが、特徴量が以前よりもだいぶ大きくなってきました。相関係数を計算して、どの変数が金相場と関係が強そうかみてみようと思います。

library(tidyverse)
 library(clipr)
 library(glmnet)
 library(patchwork)
 theme_set(theme_bw())

d <- read.csv('https://raw.githubusercontent.com/maruko-rosso/datasciencehenomiti/master/data/gold/1540_20220625.csv',encoding = 'UTF-8')

#### 前処理 ####
## NAの穴埋め 影響少ないように中央値で穴埋め
d$NYダウ終値[is.na(d$NYダウ終値)] <- median(d$NYダウ終値,na.rm = T)
d$NYダウ出来高[is.na(d$NYダウ出来高)] <- median(d$NYダウ出来高,na.rm = T)

#### 相関係数 ####
d.cor <- cor(d[,2:10])
d.cor <- round(d.cor,2)
d.cor[,1] %>% data.frame()

## gold_終値            1.00
## gold_出来高          0.40
## ドル円終値          0.90
## NYダウ終値         -0.68
## NYダウ出来高       -0.11
## 長期国債先物終値   -0.82
## 長期国債先物出来高 -0.10
## 日経平均終値       -0.55
## 日経平均_出来高      0.16

結果をみるとドル円との正の相関が非常に強く、長期国債先物とは負の相関が強いということがわかります。

相関係数を推移でみてみる

データの期間内での相関係数をみることはできましたが、長期で継続して見続けるわけにもいきませんし、さかのぼろうと思うとかなり長期間でみなければいけません。これはこれで不都合があるため、相関係数を一定期間に絞っておいかけてみようと思います。

改良の余地はたぶんにありそうですが以下が20営業日を抽出した相関係数の推移データを使ったものになります。

為替相場のみ可視化してみましょう。

## 為替
i <- 0
cor_term <- 1:20

for (i in 0:129) {
  cor_term <- 1:20
  cor_term <- cor_term + i
  cor_tbl <- d[cor_term,c(2,4)]
  cor_graph[20 + i,11] <- cor(cor_tbl)[1,2]
}
## 出来高
i <- 0
cor_term <- 1:20

for (i in 0:129) {
  cor_term <- 1:20
  cor_term <- cor_term + i
  cor_tbl <- d[cor_term,c(2,3)]
  cor_graph[20 + i,12] <- cor(cor_tbl)[1,2]
}
## NYダウ
i <- 0
cor_term <- 1:20

for (i in 0:129) {
   cor_term <- 1:20
   cor_term <- cor_term + i
   cor_tbl <- d[cor_term,c(2,5)]
   cor_graph[20 + i,13] <- cor(cor_tbl)[1,2]
 }

## 可視化
 p1 <-    cor_graph %>% 
   ggplot(aes(x = as.Date(date),y = gold_終値)) +
   geom_line() +
   scale_x_date(date_breaks = "2 week",
                date_labels = "%m/%d"
   ) +
   xlab('日付') + 
   scale_color_brewer(palette = "Set1") +
   # geom_smooth(method = lm) +
   ggtitle('1540 金相場の推移 モデル結果の反映')
 p2 <-    cor_graph %>% 
   ggplot(aes(x = as.Date(date),y = ドル円_終値)) +
   geom_line() +
   scale_x_date(date_breaks = "2 week",
                date_labels = "%m/%d"
   ) +
   xlab('日付') + 
   scale_color_brewer(palette = "Set1") +
   # geom_smooth(method = lm) +
   ggtitle('為替(ドル円)の推移')
 p3 <-    cor_graph %>% 
   ggplot(aes(x = as.Date(date),y = V11)) +
   geom_line() +
   scale_x_date(date_breaks = "2 week",
                date_labels = "%m/%d"
   ) +
   xlab('日付') + 
   ylab('相関係数の推移 20日間') + 
   scale_color_brewer(palette = "Set1") +
   # geom_smooth(method = lm) +
   ggtitle('金相場と為替の推移')
 p1 + p2 + p3 + plot_layout(ncol = 1)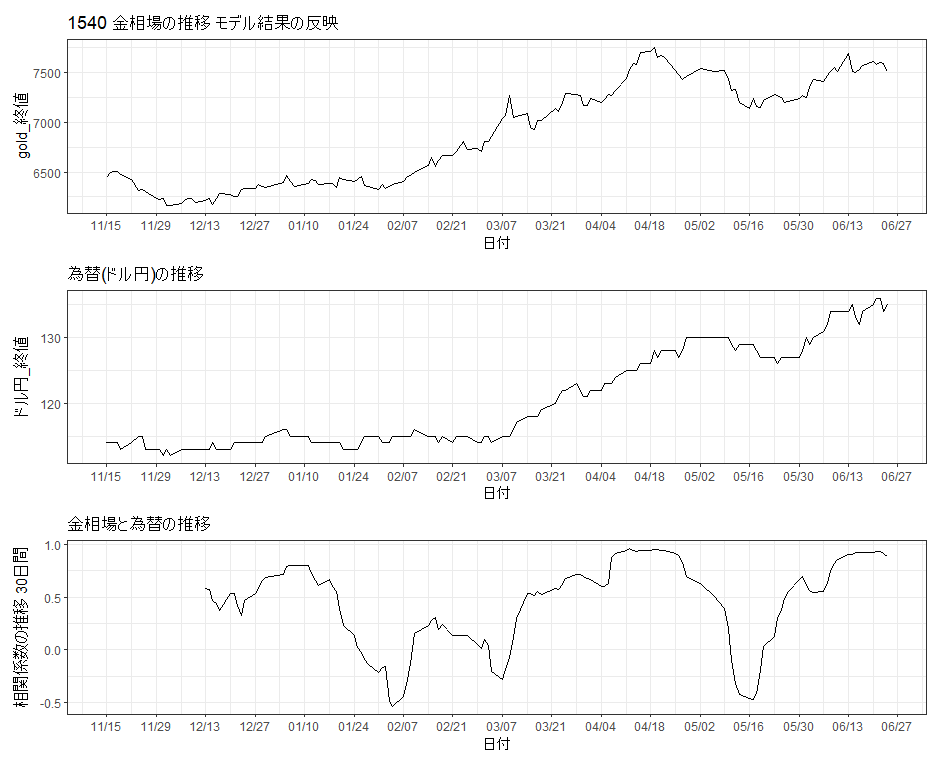

相関係数の推移をみると、為替の上げ下げと相関係数の強弱が連動が強そうです。

回帰分析の実行

他の説明変数の可視化は省略しますが、関連性が強いのを確認できたので重回帰分析を実行しようと思います。

## 重回帰分析
# 説明変数追加
 d_lm_01 <- lm(formula = gold_終値 ~ as.Date(date) ,data = cor_graph)
 d_lm_02 <- lm(formula = gold_終値 ~ as.Date(date) + gold_出来高 ,data = cor_graph)
 d_lm_03 <- lm(formula = gold_終値 ~ as.Date(date) + gold_出来高 + ドル円終値,data = cor_graph)
d_lm_04 <- lm(formula = gold終値 ~ as.Date(date) + gold_出来高 + ドル円終値 + NYダウ終値,data = cor_graph)
 summary(d_lm_03)
 summary(d_lm_04)

# Call:
#  lm(formula = gold_終値 ~ as.Date(date) + gold_出来高 + ドル円終値 +      NYダウ終値, # data = cor_graph)
#  Residuals:
#      Min      1Q  Median      3Q     Max 
#  -360.21 -103.94  -12.64   99.30  309.11 
#  Coefficients:
#                  Estimate Std. Error t value Pr(>|t|)    
#  (Intercept)   -7.790e+04  9.554e+03  -8.153 1.58e-13 ***
#  as.Date(date)  4.099e+00  5.138e-01   7.978 4.24e-13 ***
#  gold_出来高    1.806e-03  1.693e-04  10.667  < 2e-16 ***
#  ドル円_終値    3.621e+01  4.145e+00   8.734 5.69e-15 ***
#  NYダウ_終値    6.178e-02  1.208e-02   5.114 9.88e-07 ***
#  Signif. codes:  0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
#  Residual standard error: 139.8 on 144 degrees of freedom
#  Multiple R-squared:  0.9265,    Adjusted R-squared:  0.9245 
#  F-statistic: 454.1 on 4 and 144 DF,  p-value: < 2.2e-16

採用した変数はどれも有意に働いていそうです。

予測結果の可視化

作成しているグラフコードは少し冗長になるため割愛しています。

# モデル結果の格納
 cor_graph$model_01 <- d_lm_01$fitted.values
 cor_graph$model_02 <- d_lm_02$fitted.values
 cor_graph$model_03 <- d_lm_03$fitted.values
 cor_graph$model_04 <- d_lm_04$fitted.values

## 可視化
 p6 <-   cor_graph %>% 
   ggplot(aes(x = as.Date(date),y = gold_終値, col = '金相場1540')) +
   geom_line() +
   scale_x_date(date_breaks = "2 week",
                date_labels = "%m/%d"
   ) +
   xlab('日付') + 
   scale_color_brewer(palette = "Set1") +
   ggtitle('1540 金相場の推移 モデル結果の反映') +
   geom_line(aes(y = model_04,x = as.Date(date),col = 'model_04'))
 p6  + p2 + p4 + p7 + plot_layout(ncol = 2)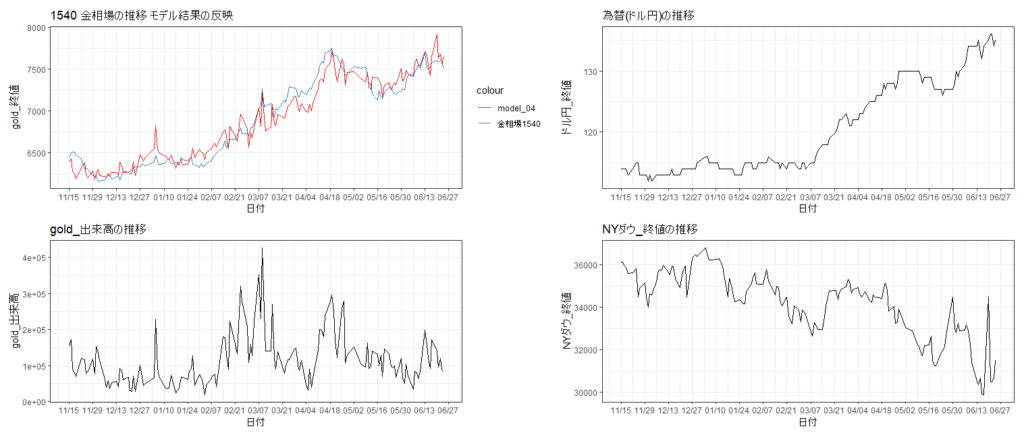

グラフにすると前回記事よりもどんどんと精度がよくなっている気がします。RMSEでの評価もみてみましょう。

## RMSE
sqrt(sum((cor_graph$gold_終値 - d_lm_01$fitted.values) ^2) / length(cor_graph$gold_終値))
#   [1] 203.9247
sqrt(sum((cor_graph$gold_終値 - d_lm_02$fitted.values) ^2) / length(cor_graph$gold_終値))
#   [1] 177.8737
sqrt(sum((cor_graph$gold_終値 - d_lm_03$fitted.values) ^2) / length(cor_graph$gold_終値))
#   [1] 149.4158
 sqrt(sum((cor_graph$gold_終値 - d_lm_04$fitted.values) ^2) / length(cor_graph$gold_終値))
#  [1] 137.453

変数を増やしたほうがより精度は高くなるようです。とはいえ、期間をしれっと伸ばすことを行っているのため、このできあがったモデル自体が有効なのかどうかというのは非常に気になります。次回は作ったモデルを使ってどの時期であっても十分な予測精度がでるのかどうかを検証してみたいなと思います。

金相場との相関関係を確認する

相関係数を推移でみてみる

回帰分析の実行

予測結果の可視化

Related posts: